5.13 Flernivåanalyse
Gjennom kommandoen regress-mml kan du foreta flernivåanalyser med inntil tre nivåer. Denne typen analyse lar deg sjekke sammenhenger knyttet til både individuelle og grupperelaterte egenskaper.
Flernivåanalyser, også kjent som hierarkiske lineære modeller eller mixed effects models, er en type statistisk analyse som tar hensyn til naturlig hierarki eller gruppering i dataene. For eksempel, studenter (nivå 1) kan være gruppert i klasser (nivå 2), som igjen er gruppert i skoler (nivå 3). Flernivåanalyser lar deg undersøke hvordan variabler på forskjellige nivåer påvirker utfallsvariabelen, og hvordan effekter kan variere mellom grupper.
Mens vanlige lineære regresjonsmodeller (OLS) lar deg analysere individuelle egenskapers effekt p�å en utfallsvariabel, kan du gjennom flernivåanalyser i tillegg studere effekter knyttet til gruppeegenskaper. Flernivåanalyser kan ses på som en avansert versjon av OLS ved at man kan studere data organisert på mer enn ett nivå.
Ved valg av gruppevariabler i en flernivåanalyse, er det viktig å tenke på følgende:
-
Teoretisk forståelse: Gruppevariabelen bør være meningsfull i forhold til det du skal analysere
-
Hierarki: Gruppevariablene bør ha en hierarkisk oppbygning. For eksempel, kan man analysere elever (nivå 1) som grupperes i skoler (nivå 2) som igjen grupperes i distrikter (nivå 3).
-
Variasjon mellom og innenfor grupper: Det bør være tilstrekkelig variasjon både mellom gruppene (for å kunne estimere gruppeeffekter) og innenfor gruppene (for å kunne estimere individuelle effekter).
-
Gruppestørrelse: Gruppene bør ikke være for små, fordi det kan gjøre det vanskelig å estimere gruppeeffekter pålitelig. Det bør være nok observasjoner innenfor hver gruppe til å gi pålitelige estimater.
-
Unngå overlapp mellom grupper: Hvis det er overlapp mellom grupper (for eksempel, hvis enkeltpersoner kan være medlem av flere grupper), kan det være mer hensiktsmessig å modellere dem som kryssede effekter i stedet for nøstede effekter. Kommandoen
regress-mmltillater per i dag ikke kryssede effekter.
For å undersøke om en kategorisk variabel egner seg som gruppevariabel, kan man bruke kommandoene boxplot eller histogram. Du bruker da utfallsvariabelen som argument, og gruppevariabelen til å gruppere fremvisningen. Eksempel:
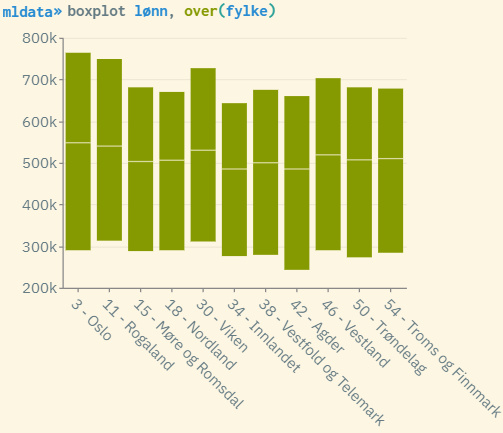
Ved å bruke kommandoen tabulate fylke, summarize(lønn) std, vises konkrete tall på standardavvik for responsvariabelen lønn fordelt på hver gruppe i gruppevariabelen fylke (overordnet standardavvik for lønn finner du nederst i samme tabell). Det samme kan gjøres for eventuelt andre gruppevariabler man vil sammenlikne med, som f.eks. landsdel.
Kommandoen regress lar deg kjøre en vanlig lineær regresjon. Dette er i praksis en ettnivåmodell som kan fungere som referanse for estimatene du får når du kjører flernivåanalyser gjennom kommandoen regress-mml. Eksempel:
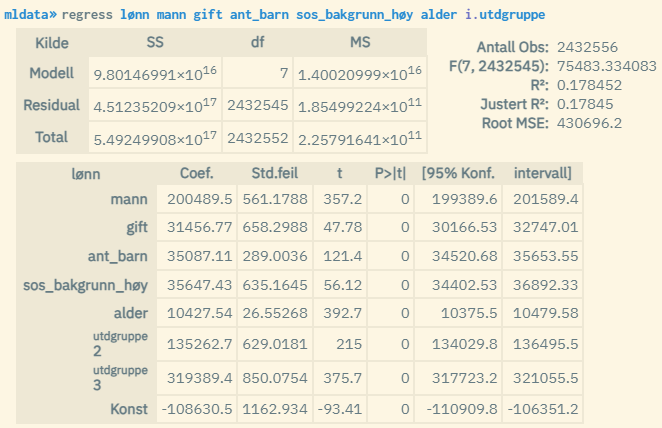
Flernivåanalyser kan kjøres på nesten samme måte som for regress. Du kjører i stedet kommandoen regress-mml der du oppgir gruppevariabel etter et by-ledd i modelluttrykket. Eksempel på tonivåmodell der bostedsfylke utgjør nivå to:
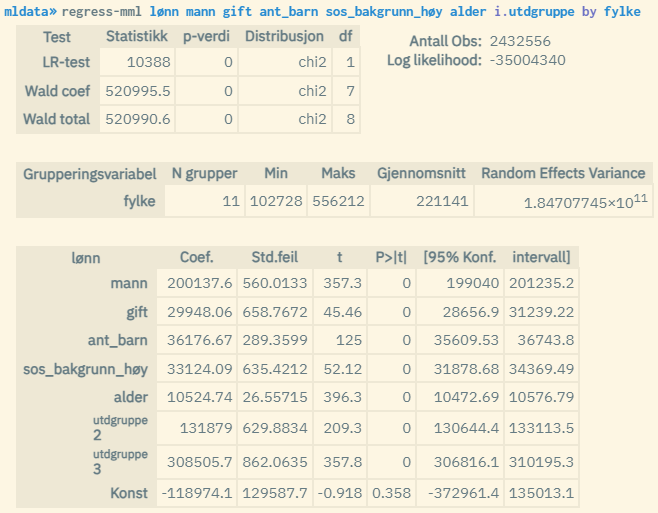
Ved å oppgi to gruppevariabler kan man kjøre en trenivåmodell. Dette er det høyeste tillatte nivået. Husk at gruppevariabel som definerer det høyeste hierarkinivået skal oppgis først. Eksempel der man bruker utdanningsnivå og hierarkisk yrkesgruppe som hhv. nivå 3 og 2:
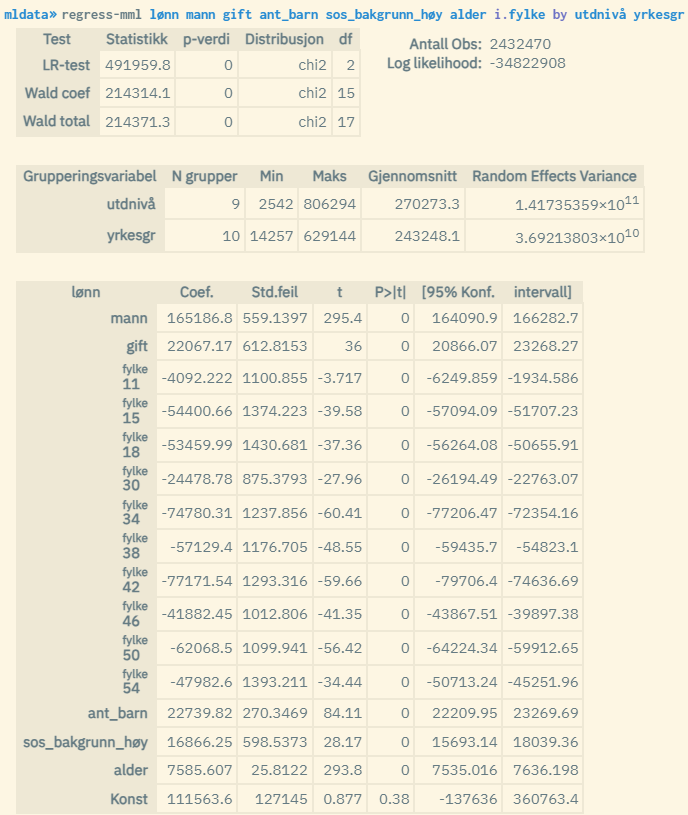
Forklaring til resultatene:
-
Antall Obs: Totalt antall enheter (vanligvis personer) som benyttes i analysen (N)
-
Log Likelihood: Log Likelihood-verdi basert på Restricted/Residual Maximum Likelihood-estimering. Gir et mål på hvor godt modellen passer til dataene (viser ofte negative verdier, og jo høyere tall (mindre negativ) dess bedre er modellen)
-
LR-test: Test for forklaringskraft i forhold til en standard OLS-estimering uten gruppevariabler (jo høyere statistikkverdi dess bedre). p-verdi < 0.05 betyr at flernivåmodellen gir signifikant bedre forklaring av total varians. df = antall frihetsgrader = antall gruppevariabler (maks 2)
-
Wald coef: Wald-test for forklaringskraften til forklaringsvariablene (jo høyere statistikkverdi dess bedre). p-verdi < 0.05 betyr at effekten av forklaringsvariablene samlet sett er signifikant forskjellige fra 0. df = antall frihetsgrader = antall forklaringsvariabler
-
Wald total: Wald-test der også gruppevariablene inngår i testen.
-
N grupper: Antall grupper for hver gruppevariabel
-
Min: Minste antall gruppeenheter for hver gruppevariabel
-
Maks: Høyeste antall gruppeeenheter for hver gruppevariabel
-
Gjennomsnitt: Gjennomsnittlig antall enheter i hver gruppe, for hver gruppevariabel
-
Random Effects Variance: Samlet mål på variansen til den avhengige variabelen for hvert nivå representert ved gruppevariablene. Jo høyere verdi, dess større del av den totale variansen kan forklares av gruppevariablene. Verdien kan ses i sammenheng med SS-verdiene for total modell (Total Sum of Squares) som rapporteres gjennom vanlig OLS-analyse (kjør da
regressmed samme variabeloppsett minus gruppevariabler). Da får man et anslag på hvor stor del av den totale varians som kan tilskrives gruppeeffekter.
Praktiske eksempler: Skript for gjenskaping av analysene det refereres til i eksemplene over
Kilde:
Algoritmene for kommandoen regress-mml baserer seg på regresjonsklassen mixedlm i Python-pakken statsmodels: https://www.statsmodels.org/devel/generated/statsmodels.regression.mixed_linear_model.MixedLM.html